Calculadora de Tonicidade/Fonicidade
Introdução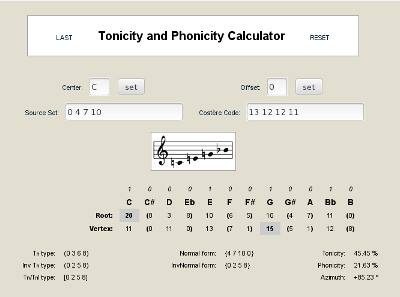
Este projeto, desenvolvido em 2013 pelo Prof. Dr. Marcus Alessi Bittencourt, apresenta uma modelagem computacional em PHP das teorias musicais psicoacústicas de Richard Parncutt (Parncutt 1988, 1989, 1997 e 2009) e de algumas de suas próprias teorias analíticas musicais (Bittencourt 2011), combinadas à Teoria Musical dos Conjuntos (Forte, 1973 e Rahn, 1980). Esta modelagem foi implementada na forma de uma calculadora analítica tornada pública à comunidade pela internet como uma página em HTML. Tal ferramenta permite o rápido acesso aos diagnósticos analíticos gerados pelo modelo computacional por meio de uma página de HTML contendo um formulário conciso e de fácil visualização e impressão.
- Ver o artigo apresentado no II Encontro Internacional de Teoria e Análise Musical de 2011, São Paulo-SP, Brasil, que contém uma introdução básica às teorias que são modeladas computacionalmente por esta calculadora.
- Ver o artigo que contém o referencial teórico e a explicação formal dos modelos matemáticos utilizados por esta calculadora.
- Versão online da calculadora.
O projeto da calculadora analítica
O estudo das propriedades combinatórias e de equivalência entre diversas coleções de alturas, grafando seus fluxos de atração e seus potenciais de invariância sob processos de transposição e inversão é uma tarefa importantíssima para trabalhos analíticos e composicionais. No entanto, tal metodologia de análise requer a realização de uma certa quantidade de cálculos que, apesar de não serem tão complexos do ponto de vista dos matemáticos, são certamente entediantes e dispendiosos do ponto de vista dos músicos. A simples consulta às "Table Synoptique des 351 Échelonnements" e "Tableaux Analytiques des Échelonnements" do "Lois et Styles" de Costère (Costère, 1954) ou às tabelas dos livros de Straus (Straus, 1990) ou Forte (Forte, 1973) também não providencia um acesso muito conveniente ao estudo de coleções de altura-classe e foi com este problema em mente que foi criada a calculadora: para providenciar um acesso rápido e claro às interpretações e diagnósticos feitos a partir da análise dos dados musicais submetidos pelo usuário. O projeto foi implementado em PHP para que a calculadora fosse absolutamente multi-plataforma e terminasse acessível a toda a comunidade musical pela internet sem a necessidade de instalação de um software especial, bastando apenas o software navegador normalmente pré-existente em qualquer computador.
Referências
BITTENCOURT, M.A. Sketches for the foundations of a contemporary experimental treatise on Harmony. In: II Encontro Internacional de Teoria e Análise Musical, 2011, São Paulo-SP, Brasil. Anais do II Encontro Internacional de Teoria e Análise Musical, São Paulo-SP, Brasil, 2011.
COSTÈRE, Edmond. Lois et Styles des Harmonies Musicales. Paris: Presses Universitaires de France, 1954.
PARNCUTT, Richard. Revision of Terhardt’s Psychoacoustical Model of the Root(s) of a Musical Chord. Music Perception. Vol. 6, No. 1 (Fall), pp. 65-93, 1988.
PARNCUTT, Richard. Harmony: A Psychoacoustical Approach. Berlin: Springer-Verlag, 1989.
PARNCUTT, Richard. A model of the perceptual root(s) of a chord accounting for voicing and prevailing tonality. In LEMAN, M. (Ed.). Music, Gestalt, and computing - Studies in cognitive and systematic musicology. Berlin, Germany: Springer-Verlag, 1997, p. 181-199.
PARNCUTT, Richard. Tonal implications of harmonic and melodic Tn-types. In KLOUCHE, T. & NOLL, T. (Eds.). Mathematics and computing in music. Berlin: Springer-Verlag, 2009, p. 124-139.
RAHN, John. Basic Atonal Theory. New York: Schirmer Books, 1980.
STRAUS, Joseph Nathan. Introduction to Post-Tonal Theory. New Jersey; Prentice Hall, 1990.
